Ay 20 was definitely my favorite class this term ( although, I will admit to a bias since I'm an Astrophysics major :P ). Any class that has anything to do with space is automatically more interesting in my book. More importantly, the material was well taught and clearly presented.
Doing regular problem sets with hard deadlines is a huge part of the normal daily life of a Caltech student. Sometimes the problem sets are good at teaching the material. Sometimes they seem irrelevant. Regardless, when life becomes too hectic, there isn't always enough time to really understand the concepts behind the questions. In this class, we didn't have hard deadlines. Instead, we dedicated most of our class time as well as an additional four hours a week to problem solving in small groups. The problems were carefully picked so that instead of just speeding through proofs in books, I could see first-hand how many of the key theories/equations were derived. Whenever we'd get stuck, Professor Johnson or Jackie were always there to give us just the right amount of guidance so that we could continue solving the problem on our own. This was a completely new style of class for me, but I feel like I learned a lot more than I would have in the standard "lecture" class. Also, thanks to the partner-work, Juliette and I became good friends :]
Caltech is arguably the best place in the world to study Astrophysics. I wouldn't trade the opportunities and experiences I have here for anything. At the same time, Caltech has a terrible habit of taking a subject that I love and trying to beat that passion out of me. In my case, this was physics. I had a fairly poor physics background coming in to Caltech and have been playing catch-up in my physics classes because of it. Since Astrophysics is basically a specialized physics major, I was starting to get discouraged. Professor Johnson and Jackie had a lot of faith in me and my future as an astronomer, which was incredibly encouraging. At the beginning of term I was on the fence between staying in astrophysics and switching to regular physics. After this class, I'm definitely staying in astro :]
Another awesome part of class was getting regular visits from leading astronomers. It was really interesting to hear from very different types of people with very different career paths that were all united by their passion for astronomy. Through our interactions with them, we also learned how to approach these professionals (and that they were, in fact, just people like you and me!).
The labs were really interesting. In the first one, we measured the radius of the earth using nothing but a stopwatch and the sunset (and we got to take a trip to the beach during the school year!). For the second lab, we analyzed a picture of mercury transiting the sun to find properties of its orbit. I ended up doing a third optional lab in which I used real data online to analyze stars and find their transiting planets. The lab write ups were the most painless I've had to do in a very long time. I'm not the biggest fan of formal writing (to say the least), and I hate when the formalities of lab write-ups take away from the excitement of actually doing the lab. The labs for this class made me feel like I was solving real-world problems instead of fulfilling some class requirement that was said ages ago.
The final was also a really good gauge of what I learned in class - which was refreshing. It also left me feeling encouraged and that the amount I studied was proportional to the amount of material I understood (which isn't always the case). Instead of a usual 4+ hour take-home written exam, we had a 30 minute oral exam. This might be difficult to implement in classes that have 200 students, but it was perfect for a small class like this.
I'm going to really miss this class next term :( I hope that more of my future astro classes will be this fun!
Tuesday, December 13, 2011
Sunday, December 4, 2011
Finding Exoplanets
As a third lab, I played around with the tools on portal.lcogt.net.
First, I started off by analyzing an image of CoRoT2b. The program asked me to pick a target star (to see if it has an exoplanet), a piece of dark sky for reference, and three calibration stars. Then, using the program, I could "analyze" the image. The measurements of the light curves of the stars I picked was saved to the combined light curve. Then I repeated the first few steps with 13 different images of the same piece of the night sky.
The second step was to classify the calibrator lightcurves as being flat, having a dip, having a blip, being periodic, or just odd. I classified two of the calibrators as seeming to have dips. These curves are then contributed to the final lightcurve for further analysis.
I couldn't figure out a way to save an image of the final lightcurve, but I can just describe it. The light curve (a plot of relative brightness as a function of time) had a drop in brightness of 5.94% and a transit time of 2.306 hours.
Using the following equations, and the above measurements, we can calculate several important features of the exoplanet.
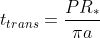
First, I started off by analyzing an image of CoRoT2b. The program asked me to pick a target star (to see if it has an exoplanet), a piece of dark sky for reference, and three calibration stars. Then, using the program, I could "analyze" the image. The measurements of the light curves of the stars I picked was saved to the combined light curve. Then I repeated the first few steps with 13 different images of the same piece of the night sky.
The second step was to classify the calibrator lightcurves as being flat, having a dip, having a blip, being periodic, or just odd. I classified two of the calibrators as seeming to have dips. These curves are then contributed to the final lightcurve for further analysis.
I couldn't figure out a way to save an image of the final lightcurve, but I can just describe it. The light curve (a plot of relative brightness as a function of time) had a drop in brightness of 5.94% and a transit time of 2.306 hours.
Using the following equations, and the above measurements, we can calculate several important features of the exoplanet.
In this case, the mass of the star was inferred to be 0.97 solar masses. The radius of the planet was found to be 2.48 Rjupiter at a distance of 0.028AU with an orbital period of 1.743 days. This seems unrealistic to me. Even just visually speaking, the light curve was pretty shallow dip. Also, .028AU is 5.6 solar Radii, which isn't a plausible distance for the orbital distance.
Although, I could have very well measured something wrong or measured the wrong star altogether. It could also be a result of poor alignment of my tags or the small sample of pictures.
The next star I looked at was HAT-P-25b. The process for this was just like that for CoRoT2b, only this time with 109 pictures instead of 13. In this case, I thought one calibrator star had no dip, one had a dip, and one had a periodic pattern. The light curve dipped 3.82% with a transit time of 2.769 hours. The size of the star is about 1.01 solar masses. Using these quantities, the planet radius is inferred to be 1.89 times that of Jupiter with an orbital radius of .047AU and an orbital period of 3.653 days.
This still feels a little strange to me, but I'm not sure where my mistake lies :/ (also, it could be that I don't have a good sense yet of the plausible properties of a transiting planet).
Overall, this lab was pretty awesome! While I was labeling all of the pictures, my room-mate walked by and asked "Are you really looking at pictures of stars again?" :)
Alternative Careers in Astrophysics
As an Astrophysics major, I feel like I subconsciously accepted the fact that I would stay in "school" for the rest of my life. In my mind, the stereotypical career path was undergrad, grad, postdoc, professorship, etc. I vividly recall talking to my relatives in the Ukraine last summer about my career path. When they asked me how many more years of school I had left, I'd answer nine (three unergrad + 6 or so for grad school) to which they'd always reply: "You mean nine months?". No. Nine years. That's a lot, considering that I've only finished 12 years up to this point. That made me start thinking about alternate career paths, which is why I wanted to cover this question of the blogging assignment.
Though I still plan on going to graduate school, I'll briefly cover the career prospects of a bachelor's degree in astrophysics. A bachelor's degree in astronomy, astrophysics (or physics) is generally not sufficient to have a research position. Alternative possibilities include being a schoolteacher, writer, museum educator, science technician, or journalist. Science technicians work alongside researchers and deal more with practical matters. It's good to note that some states require school teachers to hold a master's degree in the subject that they teach. Earning a master's degree give more career options than a bachelor's but it's still considered to have limited opportunities.
Earning a PhD in astronomy (or astrophysics) is an essential step to a solid career in astronomy. One of the many places to find jobs as an astronomer is at NASA. These range from research to management to software to engineering to data analysis. Another big-name place to work in is Lockheed Martin. Jobs there include intelligence analysis, scientist, engineer, management, and software.
Another option is to work for the military or U.S. Government. (Actually, a lot of astronomy research is government funded, so technically that's also working for the government). This doesn't necessarily mean being in the front lines. There are a lot of behind-the-scenes jobs. Personally, I really like having that option open. I don't know if I'll ever actually end up working for the military, but I've always thought that it would be really awesome. I can only imagine how confused my parents must have been when their 11-year old daughter begged them to send her to military school (lucky for me, they didn't...).
There are also career opportunities that are (seemingly) far from the astronomy field. For example, since computer programming is a skill that many astronomers share, a career as a software programmer is also a possibility. That does however, depend on the amount of programming experience included in one's research/education. Another option is to go into finance. Astronomers/astrophysicists/physicists are well known for having great analytical skills and are sought after for jobs in the finance fields.
In the last few months, I've been thinking more and more about my career. At times, I've been more than tempted to switch to physics. A lot of my peers recommend it because physics is such a broad degree name that it becomes a lot easier to find jobs in a wider selection of fields. There are also many schools (luckily Caltech isn't one of them!) where astrophysics is considered a much less rigorous major than physics. However, upon doing some reflecting I realized that regular physics doesn't interest me terribly. Or rather, I should say that the only application of physics that really excites and motivates me is that of astrophysics. I see physics as an essential tool that I need to understand stellar objects. The way physics works out is beautiful, to say the least, but all I really want to do is spend my time applying it to space-stuff.
It's great to know, however, that if somewhere down the line I can't (or choose not to) work in astronomy anymore I can take the skills I learn from it to a variety of different fields.
websites that I visited in collecting my information: monster.com, lockheedmartin.com, nasa.gov, collegeboard.com, spsnational.org,
Though I still plan on going to graduate school, I'll briefly cover the career prospects of a bachelor's degree in astrophysics. A bachelor's degree in astronomy, astrophysics (or physics) is generally not sufficient to have a research position. Alternative possibilities include being a schoolteacher, writer, museum educator, science technician, or journalist. Science technicians work alongside researchers and deal more with practical matters. It's good to note that some states require school teachers to hold a master's degree in the subject that they teach. Earning a master's degree give more career options than a bachelor's but it's still considered to have limited opportunities.
Earning a PhD in astronomy (or astrophysics) is an essential step to a solid career in astronomy. One of the many places to find jobs as an astronomer is at NASA. These range from research to management to software to engineering to data analysis. Another big-name place to work in is Lockheed Martin. Jobs there include intelligence analysis, scientist, engineer, management, and software.
Another option is to work for the military or U.S. Government. (Actually, a lot of astronomy research is government funded, so technically that's also working for the government). This doesn't necessarily mean being in the front lines. There are a lot of behind-the-scenes jobs. Personally, I really like having that option open. I don't know if I'll ever actually end up working for the military, but I've always thought that it would be really awesome. I can only imagine how confused my parents must have been when their 11-year old daughter begged them to send her to military school (lucky for me, they didn't...).
There are also career opportunities that are (seemingly) far from the astronomy field. For example, since computer programming is a skill that many astronomers share, a career as a software programmer is also a possibility. That does however, depend on the amount of programming experience included in one's research/education. Another option is to go into finance. Astronomers/astrophysicists/physicists are well known for having great analytical skills and are sought after for jobs in the finance fields.
In the last few months, I've been thinking more and more about my career. At times, I've been more than tempted to switch to physics. A lot of my peers recommend it because physics is such a broad degree name that it becomes a lot easier to find jobs in a wider selection of fields. There are also many schools (luckily Caltech isn't one of them!) where astrophysics is considered a much less rigorous major than physics. However, upon doing some reflecting I realized that regular physics doesn't interest me terribly. Or rather, I should say that the only application of physics that really excites and motivates me is that of astrophysics. I see physics as an essential tool that I need to understand stellar objects. The way physics works out is beautiful, to say the least, but all I really want to do is spend my time applying it to space-stuff.
It's great to know, however, that if somewhere down the line I can't (or choose not to) work in astronomy anymore I can take the skills I learn from it to a variety of different fields.
websites that I visited in collecting my information: monster.com, lockheedmartin.com, nasa.gov, collegeboard.com, spsnational.org,
Sunday, November 13, 2011
The Formation of Stars
(This is the write up of worksheet 10)
- The spatial scale of star formation:
- If you let the size of your body represent the size of the star forming complex, how big would the forming stars be? Let's consider a star forming region (like the Taurus region) that is about 30pc. 1 parsec is roughly 206264 AU, and 1 AU is roughly 100 solar diameters. If we consider the size of a typical star to be roughly that of the sun, a star is 1/30*20626400 in size of the star forming complex. Now let's compare this estimate to the human body. Say the average human body is 1.5 meters; then 1.5/618792000 is roughly 2.42*10^-9 meters. That's on the order of a tenth of the size of a cell membrane! That sure puts things into perspective!
- The average density of a typical star (using our sun as a model) is:
If the Taurus complex contains roughly 3*10^4 solar masses in a radius of 15 parsecs, then the average density of the region is 3.0*10^-23 times less than that of a typical star, which is roughly 1.4*10^-23 g/cm^3.
3. Proto-stars and the pre-main sequence
- The rate at which mass accumulates onto a forming star is
rearranging these equations, we find that
- To find the time it would take to build up stars of a certain mass (1 solar mass and 30 solar masses in this problem), we integrate the accretion rate with respect to time.
using cgs units where G=6.8*10^-8 cm^3/g/s^2, Msun = 2*10^33 g, and the speed of sound = 2.5*10^4cm/s , we find that it takes 8.7*10^12 seconds to build up a 1 solar mass star and 2.6*10^14 seconds to build up a 30 solar-mass star. In more familiar units, it takes roughly 2.8*10^5 years to build up a 1 solar-mass star and 8.3*10^6 years to build up a 30 solar mass star.
- The Kelvin-Helmholtz time scale is given by
In this problem, we are dealing with a 1 solar mass star (L ~ 100 solar luminosities) and a 30 solar mass star (L ~ 10^5 solar luminosities). Using the above equations and the fact that mass scales roughly as radius, we find that the Kelvin-Helmholtz time scale for the 1 solar mass star is 5.8*10^12 seconds ~ 1.8*10^5 years and the time scale for the 30 solar mass star is 1.7*10^11 seconds ~ 5.5*10^4 years. These numbers are an order of magnitude smaller than the accretion time scales. - The results from the previous part suggest that larger stars reach their main sequence faster than smaller stars. In general, larger stars have much shorter life-spans than smaller stars.
I would like to thank Juliette and Tommy for working with me!
A Starry Sky for my Room
I've been pretty busy lately, so I haven't had the chance to do very many posts. I was planning on getting to my blog earlier today, but I got side tracked. My friend and I decided to make a quick Target run. While she was looking for drawers, I came across some wall stickers. Browsing around, I found glow-in-the dark star shaped stickers!!! Needless to say, I spent the evening sticking them up on my wall. Funny enough, I had to use my Astro text book to help me reach the high spots (it's the thickest text book I own :P ).
Unfortunately, I can't find a camera that has the ability to take a photo of these in the dark - but the stars look a million times better when they glow.
Tuesday, November 8, 2011
Professional Astronomer
I've been trying to think about what it takes to be a professional astronomer since the writing assignment was posted. In general, I'm still very confused about the fine line between astronomy and astrophysics. Traditionally, astronomy is associated with observation and astrophysics is more associated with physics. However, in recent years as our knowledge of the field has greatly increased, that distinction has grown fainter and fainter. I talked to Melody about her thoughts on the subject and she explained that the difference lies in the approach. Astronomers observe the universe and use what they find to find out more about the universe. Astrophysicists use a physics approach to predict behavior of astrophysical objects.
In general, I feel like the term "Astronomer" is more like an umbrella that encompasses a lot of different types of professions and skills that ultimately serve to further our knowledge of the cosmos. For example, last summer I did an Astrophysics SURF, but most of what I did was technically computer science. However, the results contribute to the understanding of stellar objects, so it's considered as Astrophysics.
Now that I've officially put in some thought in to this, I feel like I'm more confused than I was when I started. I used to think that an Astronomer was someone who just did observing and an Astrophysicist was someone who did all the physics-y calculations. Now I see that the line between the two professions isn't as clear. So far, I consider myself an astrophysicist. I'm curious to see if that will change by the end of this assignment.
In general, I feel like the term "Astronomer" is more like an umbrella that encompasses a lot of different types of professions and skills that ultimately serve to further our knowledge of the cosmos. For example, last summer I did an Astrophysics SURF, but most of what I did was technically computer science. However, the results contribute to the understanding of stellar objects, so it's considered as Astrophysics.
Now that I've officially put in some thought in to this, I feel like I'm more confused than I was when I started. I used to think that an Astronomer was someone who just did observing and an Astrophysicist was someone who did all the physics-y calculations. Now I see that the line between the two professions isn't as clear. So far, I consider myself an astrophysicist. I'm curious to see if that will change by the end of this assignment.
Tuesday, October 25, 2011
Neutron Stars and Their Equations of State
For my summer research with LIGO, I worked a lot with neutron stars. The first portion of my project was making a mass-radius plot of different proposed equations of state. An equation of state provides the relationship between the thermodynamic variables of pressure and energy density.
I worked with/helped develop a TOV solver (which is a code in C) that makes model neutron stars (i.e. given a starting central density, outputs the properties of the resulting star). We're most interested in the masses and radii of these stars.
There were two types of equations of state: analytic and tabular. The analytic equation of state was given by the Tolman-Oppenheimer-Volkoff (TOV) equation:
![\frac{dP(r)}{dr}=-\frac{G}{r^2}\left[\rho(r)+\frac{P(r)}{c^2}\right]\left[M(r)+4\pi r^3 \frac{P(r)}{c^2}\right]\left[1-\frac{2GM(r)}{c^2r}\right]^{-1} \;](http://upload.wikimedia.org/wikipedia/en/math/9/b/d/9bd96ad49b984125129537af87edbd67.png)
It looks really scary... but luckily the program solved it, so I didn't have to :] The equation basically describes a spherically symmetric, isotropic star in static gravitational equilibrium.
The other equations of state came in the form of density-pressure tables from different researchers in the field. I wrote a function that interpolated the pressure-density relationship so that the code could use it instead of the TOV equation to create a model neutron star.
I also had to look at the constraints for the mass-radius plot.
Minimum Maximal Mass Constraint
The first constraint is based on the observation of a 2 solar-mass neutron star. Any equation of
state that does not predict a mass that reaches two solar masses is disproved by obesrvation.
General Relativity Constraint
The GR constraint requires R > 2GM/c2 because neutron stars must have a radius that
is greater than the Schwarzschild Radius. Any proposed neutron star with a radius below
the threshold would in reality be a black hole.
Finite Pressure Constraint
The finite pressure constraint, according to Lattimer and Prakash (2007) , requires
R >(9/4)GM/c2.
Causality Constraint
To obtain the causal constraint, we recreated the procedures of Koranda et al. (1997) ,
and Lattimer and Prakash (2007). To avoid a supraluminous equation of state in which
the speed of sound is faster than the speed of light, it is necessary that
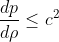
.
Rotational Constraint
For a fully relativistic star, the rotational limit can be expressed as
^{2/3}\bigg(\cfrac{M_{\mathrm{sph}}}{M_{\odot}}\bigg)^{1/3}%20km)
The final mass-radius plot that includes all of the EOS that I worked with looked like this:
I worked with/helped develop a TOV solver (which is a code in C) that makes model neutron stars (i.e. given a starting central density, outputs the properties of the resulting star). We're most interested in the masses and radii of these stars.
There were two types of equations of state: analytic and tabular. The analytic equation of state was given by the Tolman-Oppenheimer-Volkoff (TOV) equation:
![\frac{dP(r)}{dr}=-\frac{G}{r^2}\left[\rho(r)+\frac{P(r)}{c^2}\right]\left[M(r)+4\pi r^3 \frac{P(r)}{c^2}\right]\left[1-\frac{2GM(r)}{c^2r}\right]^{-1} \;](http://upload.wikimedia.org/wikipedia/en/math/9/b/d/9bd96ad49b984125129537af87edbd67.png)
It looks really scary... but luckily the program solved it, so I didn't have to :] The equation basically describes a spherically symmetric, isotropic star in static gravitational equilibrium.
The other equations of state came in the form of density-pressure tables from different researchers in the field. I wrote a function that interpolated the pressure-density relationship so that the code could use it instead of the TOV equation to create a model neutron star.
I also had to look at the constraints for the mass-radius plot.
Minimum Maximal Mass Constraint
The first constraint is based on the observation of a 2 solar-mass neutron star. Any equation of
state that does not predict a mass that reaches two solar masses is disproved by obesrvation.
General Relativity Constraint
The GR constraint requires R > 2GM/c2 because neutron stars must have a radius that
is greater than the Schwarzschild Radius. Any proposed neutron star with a radius below
the threshold would in reality be a black hole.
Finite Pressure Constraint
The finite pressure constraint, according to Lattimer and Prakash (2007) , requires
R >(9/4)GM/c2.
Causality Constraint
To obtain the causal constraint, we recreated the procedures of Koranda et al. (1997) ,
and Lattimer and Prakash (2007). To avoid a supraluminous equation of state in which
the speed of sound is faster than the speed of light, it is necessary that
.
Rotational Constraint
For a fully relativistic star, the rotational limit can be expressed as
The final mass-radius plot that includes all of the EOS that I worked with looked like this:
Hydrostatic Equilibrium and the Virial Theorem
Author: Iryna Butsky
Co-authors: Juliette Becker and Monica He
This is a write up of question 1 of the Hydrostatic Equilibrium and the Virial Theorem worksheet.
Co-authors: Juliette Becker and Monica He
This is a write up of question 1 of the Hydrostatic Equilibrium and the Virial Theorem worksheet.
- (a) We're looking for the total potential energy contained in the sun. We know that potential energy is expressed by U = - GMm/r. More specifically, in this case
where M_shell is the mass and M_int is the mass of the sphere inside that shell. We also have
and
.The change in potential energy, dU:
therefore, after combining the terms we have that
. Keeping in mind that
we can simplify the expression to
- (b) Potential energy is related to force in the following expression:
By doing dimensional analysis, we know that U has units of cm^3g^-1s^2 and dr/dt has units of cm/s. Therefore the velocity of a free-falling element would have the following relation to potential energy:
- (c) We can replace dr/dt in the equation above with
. We're assuming that the free-fall velocity will be roughly constant. Therefore, if we define tau to be the time it takes a particle to fall from the surface of the star to the center and R_solar as the radius of the Sun, then we can make this substitution to an order of magnitude.
- (d) Plugging in our values into this expression
we find that
. This means that if the Sun were truly undergoing free fall collapse, it would collapse in 34 minutes, which is surely a time-scale that we would notice.
- (e)
Saturday, October 22, 2011
Finding the Astronomical Unit

Given this image of Mercury's orbit around the sun, we need to calculate the Astronomical Unit (The distance between the Earth an the Sun). We are given that Mercury's period is 87 days and that the Sun has an angular diameter of about .5 degrees.
The diagram of this problem is represented below. The Earth is the sphere on the left, Mercury is the point M, and the sun is the right edge.
Doing a little bit of triangle geometry (the pink triangle), we can see that
Now, let's look at the blue triangle. We know that
Since theta is such a small angle, we can use the sin small angle approximation to find an expression for theta
Now let's consider the superposition of the two triangles. From this we f ind the expression:
We can plug this result back in to our previous equation to show that
Because we know the period of Mercury (87 days) and the period of the Earth (365 days), we can use that information to find the distance from the sun to Mercury, a_m
we know that a_m is just AU - x, so we can rewrite this proportion as:
we know the radius of the Earth to be 6.38*10^8 cm and alpha = 3.2*10^-5. Plugging in this messy expression into Wolfram Alpha, we find that the astronomical unit,
The real value, however, is known to be about 1.5*10^13 cm. The errors in my calculations come from my estimates in measuring alpha.
We can also use this information to find the mass of the sun.
Using Kepler's third law we have:
Using WolframAlpha once again, we find that the mass of the sun is:
This is a little off from the real value of 1.98*10^33g, but this is because our value for the AU was a little off.
Thank you Juliette and Monica for all the help!
Friday, October 21, 2011
Stellar Properties From Afar Worksheet
Author: Iryna Butsky Co-Author: Juliette Becker
- We know that the angular diameter of the sun d = 0.5 degrees. We also know that the size of the semi-major axis of the Earth's orbit around the sun, a = 1.5 x 10^13cm.
- We can now set up a simple proportion to find the radius of the sun.
- Therefore, the AU, in solar diameters is
- From Newton's version of Kepler's third law we have the following equation
 we know that P =31,556,926 secons , a = 1.5*10^13cm, and G = 6.674*10^-8 cm^3 g^-1s^-2. Plugging the numbers in we find that the mass of the Sun is about 2*10^33g.
we know that P =31,556,926 secons , a = 1.5*10^13cm, and G = 6.674*10^-8 cm^3 g^-1s^-2. Plugging the numbers in we find that the mass of the Sun is about 2*10^33g. - Using only a lightbulb and our skin, we were able to figure out the luminosity of the Sun. We are given that the power output of the light bulb is 100 W with an efficiency of .1. Therefore, the light bulb emits the equivalence of 10 W. We know that
. Therefore, we can set up a simple proportion to find the Luminosity of the sun. We decided that the energy given off from the light bulb feels roughly the same as the sun on a warm day at about 5cm distance. Therefore,
the Luminosity of the sun is about 10^26 Watts or about 10^33erg/second
- We can find the effective temperature of the sun using the equation:
We know that lambda max is equal to 500 nanometers, we find that the effective temperature of the sun is 5.8*10^3 degrees Kelvin.
- Once again, we know that
, and we found the solar luminosity to be 10^33 ergs/second. We can set up a proportion relation to find the bolometric flux at the Earth (the Solar Unit).
Therefore, the Solar Unit is 3.5*10^5 ergs/cm^2/s
Subscribe to:
Comments (Atom)




